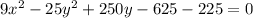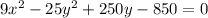Answer:
C. hyperbola;
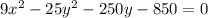
Explanation:
The given conic has equation:
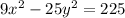
Divide through by 225.
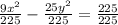
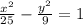
This is a hyperbola centered at the origin.
The hyperbola has been translated from the origin to (0,5).
The translated hyperbola will have equation;
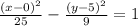
Multiply through by 225.
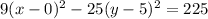
Expand
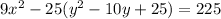
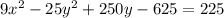
Rewrite in general form;