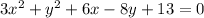Question

Q6: Identify the graph of the equation and write an equation of the translated or rotated graph in general form.

Answer 1

Answer: B) ellipse; 3x^2+y^2+6x-8y+13=0

Explanation:

Correct on edge.

Answer 2

b. ellipse;
`3x^2+y^2+6x-8y+13=0`

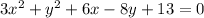
Explanation:

The given equation is

`4y^2+12x^2=24`

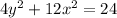
Divide through by 24;

`(y^2)/(6)+(x^2)/(2)=1`

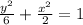
This is an ellipse that has its center at the origin.

The ellipse is translated from the origin to (-1,4).

The equation of the translated ellipse is

`((y-4)^2)/(6)+((x+1)^2)/(2)=1`

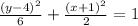
Multiply through by 6.

`(y-4)^2+3(x+1)^2=6`

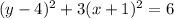
Expand;

`y^2-8y+16+3(x^2+2x+1)=6`

`y^2-8y+16+3x^2+6x+3=6`

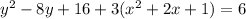
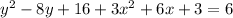
This implies that;

`3x^2+y^2+6x-8y+13=0`