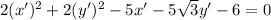Question

Q3: Identify the graph of the equation and write and equation of the translated or rotated graph in general form. (Picture Provided Below)

Answer 1

b. circle;
`2(x')^2+2(y')^2-5x'-5√(3)y'-6 =0`

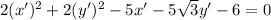
Explanation:

The given conic has equation;

`x^2-5x+y^2=3`

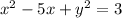
We complete the square to obtain;

`(x-(5)/(2))^2+(y-0)^2=(37)/(4)`

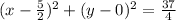
This is a circle with center;

`((5)/(2),0)`

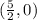
This implies that;

`x=(5)/(2),y=0`

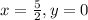
When the circle is rotated through an angle of
`\theta=(\pi)/(3)`,

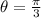The new center is obtained using;

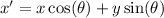`x'=x\cos(\theta)+y\sin(\theta)` and
`y'=-x\sin(\theta)+y\cos(\theta)`

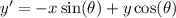
We plug in the given angle with x and y values to get;

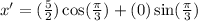`x'=((5)/(2))\cos((\pi)/(3))+(0)\sin((\pi)/(3))` and
`y'=--((5)/(2))\sin((\pi)/(3))+(0)\cos((\pi)/(3))`

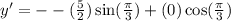
This gives us;

`x'=(5)/(4) ,y'=(5√(3) )/(4)`

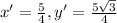
The equation of the rotated circle is;

`(x'-(5)/(4))^2+(y'-(5√(3) )/(4))^2=(37)/(4)`

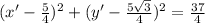
Expand;

`(x')^2+(y')^2-(5√(3) )/(2)y'-(5)/(2)x'+(25)/(4) =(37)/(4)`

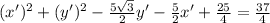
Multiply through by 4; to get

`4(x')^2+4(y')^2-10√(3)y'-10x'+25 =37`

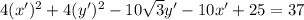
Write in general form;

`4(x')^2+4(y')^2-10x'-10√(3)y'-12 =0`

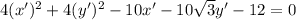
Divide through by 2.

`2(x')^2+2(y')^2-5x'-5√(3)y'-6 =0`