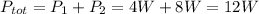Question

Two light bulbs have resistances of 400 Ω and 800 ΩThe two light bulbs are connected in series across a 120- V line. Find the current through each bulb.Enter your answers numerically separated by a comma.I 400, I 800 =______APart BFind the power dissipated in each bulb.P 400, P 800 =________WPart CFind the total power dissipated in both bulbs.P =______W

Answer 1

1) Current in each bulb: 0.1 A

The two light bulbs are connected in series, this means that their equivalent resistance is just the sum of the two resistances:

`R_(eq)=R_1 + R_2 = 400 \Omega + 800 \Omega=1200 \Omega`

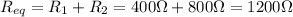
And so, the current through the circuit is (using Ohm's law):

`I=(V)/(R_(eq))=(120 V)/(1200 \Omega)=0.1 A`

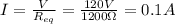
And since the two bulbs are connected in series, the current through each bulb is the same.

2) 4 W and 8 W

The power dissipated by each bulb is given by the formula:

`P=I^2 R`

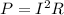
where I is the current and R is the resistance.

For the first bulb:

`P_1 = (0.1 A)^2 (400 \Omega)=4 W`

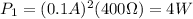
For the second bulb:

`P_1 = (0.1 A)^2 (800 \Omega)=8 W`

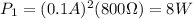
3) 12 W

The total power dissipated in both bulbs is simply the sum of the power dissipated by each bulb, so:

`P_(tot) = P_1 + P_2 = 4 W + 8 W=12 W`