Answer:
Probability of atleast one of the students(888) selecting a president with no service in the military reaches 1.
Step-by-step explanation:
Total Presidents in list = 434343
Military men to be president = 313131
Probability of selecting President who were also military men =
p = 313131/434343 = 0.72
Probability of selecting President who were not military men =
q = 1 - p = 1 - 0.72 = 0.28
Now; no of students who make a choice = 888
no. of Choices made resulting in success = x : {0, 1, 2, 3,............., 888 }
GIVEN CASE:
P(f) = Probability of atleast one student selecting a president with no service in military
This case fails when no one selects a president with no service in military, let us call it P(f').
P(f) = 1-P(f')
Calculating P(f'):
Let us define:
Failure = selecting a president with service in military , p = 0.72
Success = selecting a president with no service in military , q = 0.28
Using Binomial Theorem:
we have this case when n students make selections and x of them are successful.
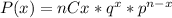
In case of f' , n = 888 and x = 0

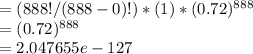
Hence, P(f') = 2.047655e-127 (reaches 0)
Now: P(f) = 1 - P(f')
P(f) = 1 - 2.047655e-127 = 1
Hence Probability of atleast one of the students(888) selecting a president with no service in the military is 1.