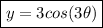Answer:
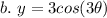
Explanation:
The cosine function is a trigonometric function whose curve is symmetric with respect to the y-axis, hence this function is said to be even. This function has the following form:
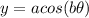
The amplitude of the plotted graph is 3 that represents half the distance between the maximum and minimum values. Since at x = 0, y = 3, this y-value is the value of a. On the other hand, the period, which is the length of one cycle of the curve, can be found as
 and:
and:

Finally: