Answer:
As the plane moves toward the listener, the apparent frequency of the plane would be
 (
(
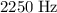 higher than the frequency at the source.)
higher than the frequency at the source.)
As the plane moves away from the listener, the apparent frequency of the plane would be approximately
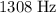 (approximately
(approximately
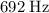 lower than the frequency at the source.)
lower than the frequency at the source.)
Assumption: the speed of sound in the air is
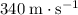 .
.
Step-by-step explanation:
Crests of this sound wave travel toward the listener at a constant
 . Since there is a pause of
. Since there is a pause of
 between every two consecutive crests of this sound wave, the distance between each pair of consecutive crests would be:
between every two consecutive crests of this sound wave, the distance between each pair of consecutive crests would be:
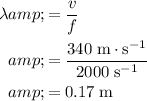 .
.
Hence, if the aircraft wasn't moving, the first crest would have a head start of
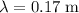 relative to the second one. This head start would ensure that the first crest arrive
relative to the second one. This head start would ensure that the first crest arrive
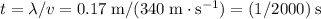 earlier than the second crest.
earlier than the second crest.
However, at a speed of
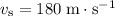 , the aircraft would have travelled an additional
, the aircraft would have travelled an additional
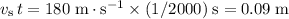 within that
within that
 .
.
- If the aircraft was travelling towards the listener, the head start of the first crest over the next one would be reduced to
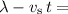
 . The first crest would arrive earlier than the second one by
. The first crest would arrive earlier than the second one by
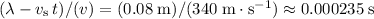 .
. - In contrast, if the aircraft was travelling away from the listener, the head start of the first crest over the next one would be increased to
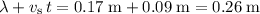 . The first crest would arrive earlier than the second one by
. The first crest would arrive earlier than the second one by
 .
.
In other words, if the aircraft was moving towards the listener, the period of the sound would appear to the listener to be approximately
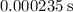 . in contrast, if the aircraft was moving away from the listener, the period of the sound would appear to the listener as approximately
. in contrast, if the aircraft was moving away from the listener, the period of the sound would appear to the listener as approximately
 .
.
Therefore:
- When the aircraft moves toward the listener, the listener would hear a frequency of
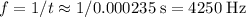 .
. - When the aircraft moves away from the listener, the listener would hear a frequency of approximately
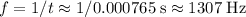 .
.