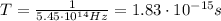Question

Light waves are electromagnetic waves that travel at 3.00 Light waves are electromagnetic waves that travel 108 m/s. The eye is most sensitive to light having a wavelength of 5.50 Light waves are electromagnetic waves that travel 10-7 m.(a) Find the frequency of this light wave.Hz(b) Find its period.s

Answer 1

(a)
`5.45 \cdot 10^(14) Hz`

The relationship between frequency and wavelength of an electromagnetic wave is given by

`c=f \lambda`

where

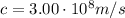`c=3.00 \cdot 10^8 m/s` is the speed of light

`f` is the frequency

`\lambda` is the wavelength

In this problem, we are considering light with wavelength of

`\lambda=5.50 \cdot 10^(-7) m`

Substituting into the equation and re-arranging it, we can find the corresponding frequency:

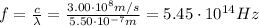
`f=(c)/(\lambda)=(3.00 \cdot 10^8 m/s)/(5.50 \cdot 10^(-7) m)=5.45 \cdot 10^(14) Hz`

(b)
`1.83\cdot 10^(-15) s`

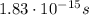
The period of a wave is equal to the reciprocal of the frequency:

`T=(1)/(f)`

And using
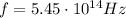`f=5.45 \cdot 10^(14) Hz` as we found in the previous part, we can find the period of this wave:

`T=(1)/(5.45 \cdot 10^(14) Hz)=1.83\cdot 10^(-15) s`