Y greater than or equal to |x| + 3 which of the following is NOT a solution of the inequality

Question

asked Oct 7, 2022 47.2k views

2 Answers

Fencekicker · Answer 1 · 2022-10-12T14:53:10+0000

Answer:

We conclude that the point (-3, 0) does NOT satisfy the inequality.

Explanation:

Given the expression

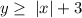
$y\ge \:\left|x\right|+3\:\:\:\:$

putting x = -3 and y = 6

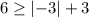
$6\ge \left|-3\right|+3\:\:\:$

Apply absolute rule: |-a| = a

$6\ge \:6$

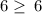
TRUE

Thus, the point (-3, 6) satisfies the inequality.

Given the expression

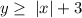
$y\ge \:\left|x\right|+3\:\:\:\:$

putting x = 0 and y = 4

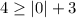
$4\ge \left|0\right|+3$

Apply absolute rule: |a| = a, a≥0

$4\ge \:3$

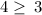
TRUE

Thus, the point (0, 4) satisfies the inequality.

Given the expression

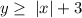
$y\ge \:\left|x\right|+3\:\:\:\:$

putting x = -3 and y = 0

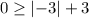
$0\ge \left|-3\right|+3\:\:\:$

Apply absolute rule: |-a| = a

$0\ge \:6$

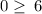
FALSE

Thus, the point (-3, 0) does NOT satisfy the inequality.

Therefore, we conclude that the point (-3, 0) does NOT satisfy the inequality.