Question

Is the following shape a right triangle? how do you know? ​

Answer 1

I would go with c. It looks like point b is where the right triangle is

Answer 2

Yes, two sides are perpendicular and the side lengths fit the Pythagoras theorem.

Explanation:

Given the triangle whose coordinates are A(0,2), B(-2, -1) and C(1, -3)

we have to find the given triangle is right angled triangle or not.

First we have to find the length of sides of triangle ABC

`\text{By distance formula, the length of line joining the points }(x_1,y_1)\text{ and }(x_2, y_2)`

`Distance=√((x_2-x_1)^2+(y_2-y_1)^2)`

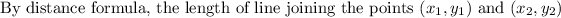
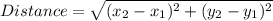
Therefore, length of AB, BC, and AC is

`AB=√((-2-0)^2+(-1-2)^2)=√(4+9)=√(13) units`

`BC=√((1-(-2))^2+(-3-(-1))^2)=√(9+4)=√(13) units`

`AC=√((1-0)^2+(-3-2)^2)=√(1+25)=√(26) units`

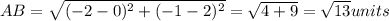
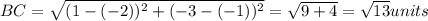
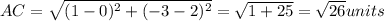
If given triangle is right angled triangle then the length of sides must satisfy Pythagoras theorem i.e

`AC^2=AB^2+BC^2`

`(√(26))^2=(√(13))^2+(√(13))^2`

`26=13+13`

`26=26`

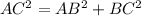
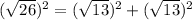
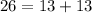
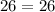
which is true.

Hence, Pythagoras theorem is satisfied.

Hence option C is correct.