Question

What kind of image is formed when an object is placed between the focal point and the vertex on the principle axis of a concave mirror ?

A. Real , inverted , & smaller
B.virtual , upright & larger
C. Real, inverted, & same size
D.virtual, upright, & same size
E. Real , upright & smaller

#PLATO!!! Help!!

Answer 1

B). virtual , upright & larger

Step-by-step explanation:

As we know by the mirror formula

`(1)/(d_i) + (1)/(d_o) = (1)/(f)`

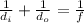
now here we will have

`d_o < f`

`d_i = ((d_o)(f))/(d_o - f)`

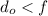
now for magnification we will have

`M = (d_i)/(d_o)`

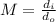
now we have

`M = (f)/((d_o - f))`

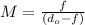
here we can say for the magnitude of magnification that it is always greater than 1 for above position of object and also it is negative which shows the image is virtual and upright.

so correct answer will be

B.virtual , upright & larger

Answer 2

Answer;

B.virtual , upright & larger

Explanation;

• When an object is placed between the focal point and vertex then a virtual image is formed behind the mirror.
• Since the rays reflected from the mirror do not intersect, their extensions behind the mirror intersect and virtual image is formed. The Image is magnified in size and erect unlike the real images.