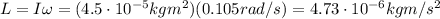Question

Find the magnitude of the angular momentum of the second hand on a clock about an axis through the center of the clock face. The clock hand has a length of 15.0 cm and a mass of 6.00 g. Take the second hand to be a slender rod rotating with constant angular velocity about one end.

Answer 1

`4.73\cdot 10^(-6) kg m/s^2`

Step-by-step explanation:

First of all, let's calculate the moment of inertia of the second hand. The moment of inertia of a slender rod rotating about one end is given by

`I=(1)/(3)mL^2`

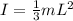
where m is the mass of the rod and L is its length. For the second hand, we have

m = 6.00 g = 0.006 kg

L = 15.0 cm = 0.15 m

So, the moment of inertia is

`L=(1)/(3)(0.006 kg)(0.15 m)^2=4.5\cdot 10^(-5) kg m^2`

Then, we have to calculate the angular speed of the second hand, which is given by:

`\omega = (2 \pi)/(T)`

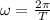
where T is the period of the second hand, which is T=60 s. Substituting,

`\omega = (2 \pi)/(60 s)=0.105 rad/s`

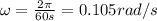
Now we can finally calculate the angular momentum of the second hand, which is equal to the product of the moment of inertia I and the angular speed
`\omega`:

`L=I\omega =(4.5\cdot 10^(-5) kg m^2)(0.105 rad/s)=4.73\cdot 10^(-6) kg m/s^2`