So you have x^3 - 4x = 0. What you can do is pull out an x from both x^3 and - 4x so it looks like this:
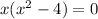
Then you can find a number that makes the part inside the parentheses turn into zero. For beginners, it may be easier to write it out seperately and solve for x.
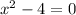
We need to solve for x, so the first step is to add 4 to both sides, so we get something like this:
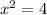
Then, we can square root both sides to get rid of the power on the x, so it looks like this:

Now, every square root has two answers, a positive and a negative. If we look at the bottom example:
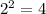
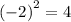
We can see that both -2 and 2 to the power of two will equal to 4.
So finally, we get:
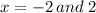
These are the other 'Zero's for the original function. If you are not sure of what a 'Zero' is, it is where the function crosses over the x-axis on a graph.