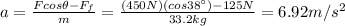Question

A worker drags a crate across a factory floor by pulling on a rope tied to the crate (Fig. 6-60). The worker exerts a force of 450 N on the rope, which is inclined at 38� to the horizontal, and the floor exerts a horizontal force of 125 N that opposes the motion.

(a) Calculate the magnitude of the acceleration of the crate if its mass is 325 kg.
m/s2
(b) Calculate the acceleration if the crate's weight is 325 N.
m/s2

Answer 1

(a) 0.71 m/s^2

We are only interested in the horizontal motion of the crate, so there are two forces acting on the crate along this direction:

- The horizontal component of the force exerted by the worker through the rope, which is given by

`F cos \theta`

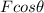
where F = 450 N and
`\theta=38^(\circ)`

- The horizontal force of friction that opposes the motion, given by

`F_f = 125 N`

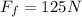
The two forces have opposite directions, so we must take into account a negative sign. According to Newton's second law, the resultant of these forces is equal to the product between the mass of the crate, m, and its acceleration, a:

`F cos \theta - F_f = ma`

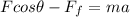
where m = 325 kg. Re-arranging the equation, we can find the magnitude of the acceleration:

`a=(F cos \theta - F_f)/(m)=((450 N)(cos 38^(\circ))-125 N)/(325 kg)=0.71 m/s^2`

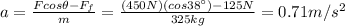
(b) 6.92 m/s^2

In this case, we need to find the mass of the crate first. We know that its weight is given by

`W=mg`

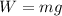
where g=9.8 m/s^2 is the acceleration due to gravity. Since we know W=325 N, we find

`m=(W)/(g)=(325 N)/(9.8 m/s^2)=33.2 kg`

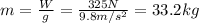
And now we can use the same equation used in part (a) to find the acceleration of the crate:

`a=(F cos \theta - F_f)/(m)=((450 N)(cos 38^(\circ))-125 N)/(33.2 kg)=6.92 m/s^2`