Question

Calculate the perimeter of this sector. ​

Answer 1

The two straight edges of the shape correspond to the original circle's radius, 5.5 cm. We're told this sector has area 30.25 cm^2, which we will use to determine the measure of the central angle subtended by the arc (the remaining edge of the shape).

The complete circle has an area of
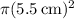`\pi(5.5\,\rm cm)^2`, which corresponds to a "central angle" of
`2\pi\,\rm rad`. Then if
`\theta` is the central angle of this sector, we have

`(\pi(5.5\,\rm cm)^2)/(2\pi\,\rm rad)=\frac{30.25\,\mathrm{cm}^2}\theta\implies\theta=2\,\mathrm{rad}`

The complete circle has a circumference of
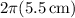`2\pi(5.5\,\rm cm)`. Then if
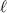`\ell` is the length of the sector's arc, we get

`(2\pi(5.5\,\rm cm))/(2\pi\,\rm rad)=(\ell)/(2\,\rm rad)\implies\ell=11\,\rm cm`

So the sector has a total perimeter of

5.5 cm + 5.5 cm + 11 cm = 22 cm