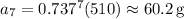A decay rate of 26.3% per minute means that for every minute that passes, there remains 73.7% of the amount of the substance available at the end of the previous minute.
If
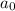 is the starting amount, and
is the starting amount, and
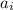 is the amount left after
is the amount left after
 minutes, then
minutes, then
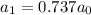
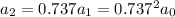
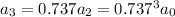
and so on, such that
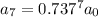
We have
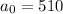 grams at the start, so after 7 minutes we're left with
grams at the start, so after 7 minutes we're left with