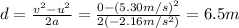Answer:
6.5 m
Step-by-step explanation:
First of all, we need to compute the acceleration of the skier. We know that there is only force acting on the skier: the force of friction, which is in the opposite direction to the motion of the skier. Using 2nd Newton Law:

where
 is the force of friction, with
is the force of friction, with
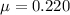 is the coefficient of kinetic friction
is the coefficient of kinetic friction
m is the mass of the skier
 is the acceleration due to gravity
is the acceleration due to gravity
Re-arranging the equation, we find:
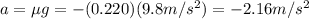
So now we can use the following SUVAT equation to calcualte the total displacement of the skier before stopping:

where
v = 0 is the final velocity
u = 5.30 m/s is the initial velocity
a = -2.16 m/s^2 is the acceleration
d = ? is the displacement
Solving the formula for d, we find: