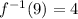Answer:
Part 1) No
Part 2) Option 4.
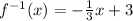
part 3)
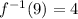
Explanation:
Part 1) we have
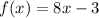
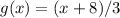
Find the inverse of f(x) and then compare with g(x)
Let
y=f(x)
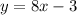
Exchange the variables x for y and y for x
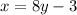
Isolate the variable y
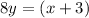
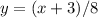
Let
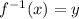
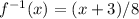
therefore
the functions f(x) and g(x) are not inverses of each other
Part 2) we have
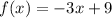
Let
y=f(x)
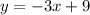
Exchange the variables x for y and y for x
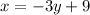
Isolate the variable y
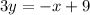
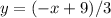
Let
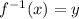
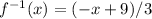
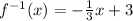
Part 3) we know that
For
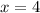 ,
,
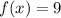
so
For
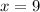 ,
,