Question

Check all of the polynomial functions that have 2 as a root. h(m) = 8 – m3 f(g) = g3 – 2g2 + g f(a) = a3 – 4a2 + a + 6 f(x) = x3 – x2 – 4

Answer 1

Answer: On ed2020, the correct answers are A, C and D

Explanation:

Answer 2

Option A , C and D are correct

Explanation:

If x = a is the root of the polynomial p(x)

then;

p(a) = 0

Given that:

The polynomial functions that have 2 as a root.

Option A:

`h(m) =8-m^3`

if 2 is the root of the polynomial h(m) then;

`h(2) =8-2^3=8-8=0`

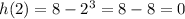
⇒h(m) is the polynomial functions that have 2 as a root.

Option B.

`f(g) =g^3-2g^2+g`

Put g = 2

then;

`f(2) = 2^3-2(2)^2+2 = 8-8+2 = 2\\eq 0`

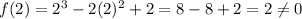
⇒f(g) is the polynomial functions that does not have 2 as a root.

Option C:

`f(a) =a^3-4a^2+a+6`

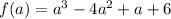
Put a = 2

then;

`f(2) =2^3-4(2)^2+2+6=8-16+8 = 16-16 = 0`

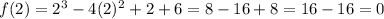
⇒f(a) is the polynomial functions that have 2 as a root.

Option D:

`f(x) =x^3-x^2-4`

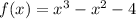
Put x= 2

then;

`f(2) =2^3-2^2-4=8-4-4 =8-8 = 0`

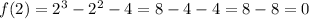
⇒f(x) is the polynomial functions that have 2 as a root.