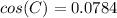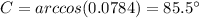Answer:
The measures of the angles at its corners are
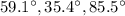
Explanation:
see the attached figure to better understand the problem
step 1
Find the measure of angle A
Applying the law of cosines
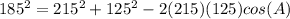
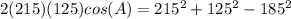
![cos(A)= [215^(2)+125^(2)-185^(2)]/(2(215)(125))](https://img.qammunity.org/2020/formulas/mathematics/middle-school/rvpsh61dvid2jkhdpa2tfza5ttdvi6z50d.png)
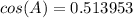
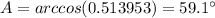
step 2
Find the measure of angle B
Applying the law of cosines
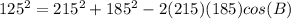
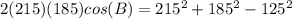
![cos(B)= [215^(2)+185^(2)-125^(2)]/(2(215)(185))](https://img.qammunity.org/2020/formulas/mathematics/middle-school/7rxy2vt3w0f3av3cq7i3jax91eff5kjj07.png)
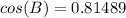
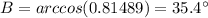
step 3
Find the measure of angle C
Applying the law of cosines
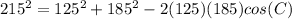
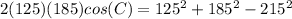
![cos(C)= [125^(2)+185^(2)-215^(2)]/(2(125)(185))](https://img.qammunity.org/2020/formulas/mathematics/middle-school/88i8s0pnlemjjzf1zh7yy4ro5jivt5ensw.png)