Question

On a balanced seesaw, a boy three times as heavy as his partner sits

1/3 the distance from the fulcrum
less than 1/3 the distance from the fulcrum
more than 1/3 the distance from the fulcrum

Answer 1

1/3 the distance from the fulcrum

Step-by-step explanation:

On a balanced seesaw, the torques around the fulcrum calculated on one side and on another side must be equal. This means that:

`W_1 d_1 = W_2 d_2`

where

W1 is the weight of the boy

d1 is its distance from the fulcrum

W2 is the weight of his partner

d2 is the distance of the partner from the fulcrum

In this problem, we know that the boy is three times as heavy as his partner, so

`W_1 = 3 W_2`

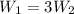
If we substitute this into the equation, we find:

`(3 W_2) d_1 = W_2 d_2`

and by simplifying:

`3 d_1 = d_2\\d_1 = (1)/(3)d_2`

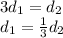
which means that the boy sits at 1/3 the distance from the fulcrum.