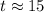Question

A scientist is growing bacteria in a lab for study. One particular type of bacteria grows at a rate of y=2t^2+3t+500. A different bacteria grows at a rate of y=3t^2+t+300. In both of these eqiations y is the number of bacteria after t minutes. When is there an equal number of both types of bacteria.

Answer 1

Approximately after 15 minutes.

Step-by-step explanation

The growth rate of the first bacteria is

`y = 2 {t}^(2) + 3t + 500`

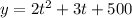
The growth rate of the first bacteria :

`y = 3 {t}^(2) + t + 300`

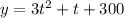
To find the time that, there will be an equal number of bacteria, we equate the two equation;

`3 {t}^(2) + t + 300 = 2 {t}^(2) + 3t + 500`

`3 {t}^(2) - 2 {t}^(2) + t - 3t + 300 - 500 =00`

`{t}^(2) - 2t - 200= 0`

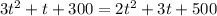
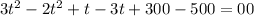
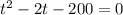
We solve for t to get,

`t = 15.177`

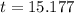
Or

`t = - 13.177`

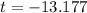
We discard the negative value.

This implies that,

`t \approx15`