Answer:
x =8
Explanation:
To answer this question you must find the point at which
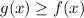
So, we have:
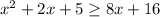
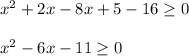
To solve the quadratic function we use the quadratic formula
±
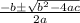
Where:
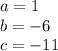
Then:
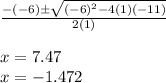
The line cuts the parabola by 2 points, x = -1.472 and x = 7.47.
You can verify that between x = -1.472 and x = 7.47. the line is greater than the parabola, but from x = 7.47, the parabola is always greater than the graph of the line.
Therefore the point sought is:
x = 7.47≈ 8