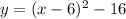Question

Write this equation in vertex form.
y = x^2 -12x +20

Answer 1

y = (x-6)²-16

Explanation:

We have given a quadratic equation.

y = x²-12x+20

We have to rewrite above equation in vertex form.

y = a(x-h)²+k is vertex form of quadratic equation.

Adding and subtracting (-6)² to both sides of above equation, we have

y = x²-12x+20+(-6)²-(-6)²

y = x²-12x+(-6)²+20-(-6)²

y = (x-6)²+20-36

y = (x-6)²-16

The vertex form is y = (x-6)²-16 where (6,16) is vertex for equation of parabola.

Answer 2

`y = (x-6) ^ 2 -16`

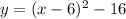
Explanation:

The vertex form for a quadratic equation has the following form:

`y = (x-h) ^ 2 + k`

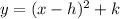
Where the vertice of the equation is the point (h, k)

To transform the equation
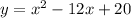`y = x ^ 2 -12x +20` in its vertex forms we must find its vertex.

Be a quadratic equation of the form:

`ax ^ 2 + bx + c`

Where a, b and c are real numbers, then the vertex of the equation will be:

`x = - (b)/(2a)`

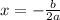
For the given equation:

`b = -12\\a = 1`

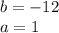
Therefore the vertice is:

`x = - (-12)/(2(1))\\\\x = 6`

Now we substitute x = 6 into the equation and find the value of k.

`y = (6) ^ 2 -12 (6) +20\\\\y = -16 = k`

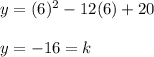
Therefore the vertice is: (6, -16)

And the equation is:

`y = (x-6) ^ 2 -16`