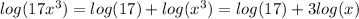Question

Which properties would you use to simplify the following expression?
log (17x^3)

Answer 1

It's 1 and 3 on edge

Explanation:

I just got it right

Answer 2

Product property of logarithms:

`log(MN)=logM+logN`

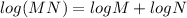
Power property of logarithms:

`log(M^(p))=plog(M)`

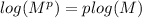
Explanation:

To solve the problem you must apply the proccedure shown below:

- Apply the Product property of logarithms, which is:

`log(MN)=logM+logN`

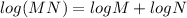
- Apply the Power property of logarithms, which is:

`log(M^(p))=plog(M)`

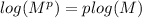
Therefore you have:

`log(17x^(3))=log(17)+log(x^(3))=log(17)+3log(x)`