Question

A man can jump 1.5 m on earth. calculate the approximate

height he might be
able to jump on
a planet whose
density is one quarter of the earth and where radius
is one third that of earth.

Radius of earth = 6400km
Acc. due to gravity=9.8 m/s²
Mass of earth = 6X10^24 kg
​

Answer 1

18 m

Step-by-step explanation:

G = Gravitational constant

m = Mass of planet =
`\rho V`

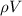
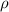`\rho` = Density of planet

V = Volume of planet assuming it is a sphere =
`(4)/(3)\pi r^3`

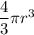
r = Radius of planet

Acceleration due to gravity on a planet is given by

`g=(Gm)/(r^2)\\\Rightarrow g=(G\rho V)/(r^2)\\\Rightarrow g=(G\rho (4)/(3)\pi r^3)/(r^2)\\\Rightarrow g=(4G\rho\pi r)/(3)`

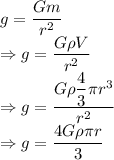
So,

`g\propto \rho r`

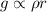
Density of other planet =
`\rho_p=(1)/(4)\rho_e`

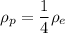
Radius of other planet =
`r_p=(1)/(3)r_e`

`(g_e)/(g_p)=(\rho_e r_e)/(\rho_p r_p)\\\Rightarrow (g_e)/(g_p)=(\rho_e r_e)/((1)/(4)\rho_e* (1)/(3)r_e)\\\Rightarrow (g_e)/(g_p)=12\\\Rightarrow g_p=(g_e)/(12)\\\Rightarrow g_p=(9.8)/(12)`

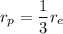
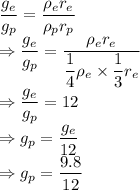
Since the person is jumping up the acceleration due to gravity will be negative.

From kinematic equations we have

`v^2-u^2=2g_es\\\Rightarrow u^2=v^2-2g_es\\\Rightarrow u^2=0-2* -9.8* 1.5\\\Rightarrow u^2=2* 9.8* 1.5`

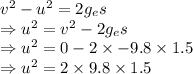
On the other planet

`v^2-u^2=2g_ps\\\Rightarrow s=(v^2-u^2)/(2g_p)\\\Rightarrow s=(0-(2* 9.8* 1.5))/(2* -(9.8)/(12))\\\Rightarrow s=18\ \text{m}`

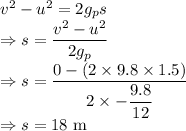
The man can jump a height of 18 m on the other planet.