Question

Please select the best answer from the choices provided

T
F

Answer 1

Yes, the answer is true.

Explanation:

We can solve the inequality by putting x=3 and y=8 in the given inequality. This is because ordered paired inequalities are denoted by (x,y). The given inequality possess the symbols for an absolute value of a number. On a number line the absolute value is the distance between the number and zero.

So, now solving the inequality, we have:

y<|x+2|+7

8<|3+2|+7

8<|5|+7

8<5+7

8<12

Hence, the statement is true - the ordered pair (3,8) is a solution to y<|x+2|+7

Answer 2

T

Explanation:

When it comes to ordered pairs in inequalities, they are represented with the (x,y) values. So the ordered pair (3,8) can be substituted in the inequality
`y<|x+2|+7`.

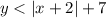In this inequality we have the symbols for an absolute value of a number. The absolute value of any integer will always be a positive integer as it is just the number of spaces from the origin (0,0).

So we can simply substitute the values of x and y like so:

`y<|x+2|+7`.

`8<|3+2|+7`.

`8<|5|+7`.

`8<5+7`.

`8<12`.

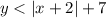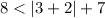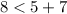This leaves us with 8<12 for the inequality making the statement true.