Question

Which of the following are square roots of —8 + 8i/3? Check all that apply.

Answer 1

Answer: b and c

Explanation:

Answer 2

Options (2) and (3)

Explanation:

Let,
`\sqrt{-8+8i√(3)}=(a+bi)`

`(\sqrt{-8+8i√(3)})^2=(a+bi)^2`

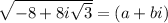
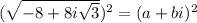
-8 + 8i√3 = a² + b²i² + 2abi

-8 + 8i√3 = a² - b² + 2abi

By comparing both the sides of the equation,

a² - b² = -8 -------(1)

2ab = 8√3

ab = 4√3 ----------(2)

a =
`(4√(3))/(b)`

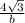
By substituting the value of a in equation (1),

`((4√(3))/(b))^2-b^2=-8`

`(48)/(b^2)-b^2=-8`

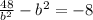
48 - b⁴ = -8b²

b⁴ - 8b² - 48 = 0

b⁴ - 12b² + 4b² - 48 = 0

b²(b² - 12) + 4(b² - 12) = 0

(b² + 4)(b² - 12) = 0

b² + 4 = 0 ⇒ b = ±√-4

b = ± 2i

b² - 12 = 0 ⇒ b = ±2√3

Since, a =
`(4√(3))/(b)`

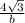
For b = ±2i,

a =
`(4√(3))/(\pm2i)`

=
`\pm(2i√(3))/((-1))`

=
`\mp 2i√(3)`

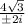
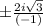
But a is real therefore, a ≠ ±2i√3.

For b = ±2√3

a =
`(4√(3))/(\pm 2√(3))`

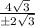
a = ±2

Therefore, (a + bi) = (2 + 2i√3) and (-2 - 2i√3)

Options (2) and (3) are the correct options.