Check the picture below, I'll be referring to the material in the picture.
we know the outer cube has a surface area of 24, we also know is a cube, so it has 6 equal sides which are squares each, let's say the side of one of those squares in the cube is say of length "s", so the area of one square will just be s², and for 6 squares that'll be an area of 6s², that is the area of the outer cube, which we know is 24.
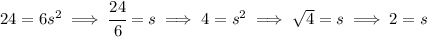
now, we know the sphere is inscribed in the outer cube, so it's touching its edges, like you see in the picture in blue, so if we get a cross-section of the whole lot, we'd get the picture to the right of blue cube in the picture, an outer cube with a side of 2, and therefore an sphere with a diameter of 2, and thus a radius of 1, as you can see in the red triangle.
Let's notice that the red triangle is a 45-45-90 triangle, and thus we can use the 45-45-90 rule to get its sides, as you can see in the picture on the far-right, which gives us half of one side of the inner cube to be 1/√2.
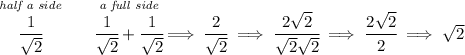
now as you can see in the picture, the inner cube in orange, has 6 sides, each side is √2 long, so let's get the 6 squares area.
