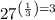Answer:
Explanation:
Given logarithmic equation is
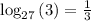
Question says to rewrite the given logarithmic equation as an exponential equation.
so we can apply transformation formula :
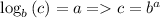
Using this formula, given problem can be transformed into exponential equation as:
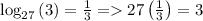
Hence final answer is