Answer:

Explanation:
To solve the exercise you must solve for b from the formula for the hypotenuse, as you can see below:
- Square both sides of the equation as following:

- Now you must subtract a² from each side of the equation, then you obtain:
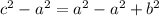
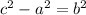
- Apply square root to both sides:

Then:
