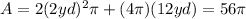Question

Use the net to find the surface area of the cylinder. Give answer in terms of pi.

Answer 1

56
`\pi`yd²

Explanation:

A=2
`\pi rh +2\pi rx^(2)`

=2×
`\pi` × 2yd ×12yd +2×
`\pi`×2yd×2yd

=48
`\pi` yd² + 8
`\pi`yd²

=56
`\pi`yd²

Answer 2

Answer: THIRD OPTION

Explanation:

To solve the exercise you must add the area of the circles (which are equal) and the area of the rectangle.

(Multiply the formula of the area of a cylinder by 2, because both are equal)

The area of a circle is:

`A=r^(2)\pi`

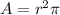
Where r is the radius

The area of a rectangle is:

`A=lw`

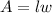
Where l is the lenght and w is the width.

The lenght of the rectagle is the circumference of the circle:

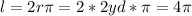`l=2r\pi=2*2yd*\pi=4\pi`yd

Then the area of the cylinder is:

`A=2(2yd)^(2)\pi+(4\pi)(12yd)=56\pi`