Question

B) The adjoining cylindrical vessel is 70 CM high and the radius

of its base is 35cm. If it contains some water up to the height
of 20 cm, how much water is required to fill the vessel
completely​

Answer 1

`\large\boxed{\pink{\sf \leadsto The \ Volume \ of \ water \ needed \ to \ be \ filled \ is \ 192,500 cm^3}}`

Explanation:

Given that , cylindrical vessel is 70 cm high and the radius of its base is 35cm . it contains some water up to the height of 20 cm .

And we need to find the water required to fill it completely .

Figure :-

`\setlength{\unitlength}{1 cm}\begin{picture}(12,12)\linethickness{0.4mm}\put(0,0){\line(0,1){5}} \put(3,0){\line(0,1){5}}\qbezier(0,5)(1.5,4)(3,5)\qbezier(0.001,0)(1.5,1)(3,0)\qbezier(0,5)(1.5,6)(3,5)\qbezier(0.001,0)( 1.5, - 1)(3,0)\put(3.5,2){\vector(0,-1){2}}\put(3.5,3){\vector(0,1){2}}\put(3.5,2.5){$\sf 70 cm $}\put(1.4,0){\line(1,0){1.6}} \put(1.4,0.2){$\sf 35cm$}\qbezier(0,2.5)(1.5,3.5)(3,2.5)\qbezier(0,2.5)(1.5, 1.8)(3,2.5)\put(-1,1){\vector(0,-1){1}}\put(-1,1.5){\vector(0,1){1}}\put(-1.3,1.2){$\sf 20cm $}\end{picture}`

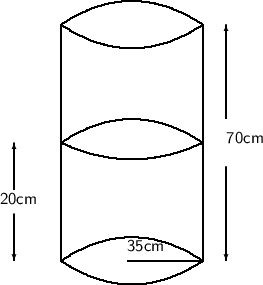
Let us take the Volume of Cylinder be V and the volume of cylinder filled be v . Let the volume required to be filled be X .

From the figure it's clear that , Volume of water required to fill the cylindrical vessel completely will be :-

`\tt:\implies v + x = V \:\: \bigg\lgroup \red{\bf As \ per \ our \ assumption }\bigg\rgroup \\\\\tt:\implies x = V - v \\\\\tt:\implies x = \pi r^2 H - \pi r^2 h \\\\\tt:\implies x = \pi r^2 ( H - h ) \\\\\tt:\implies x = \pi r^2 ( 70 cm - 20 cm ) \\\\\tt:\implies x = (22)/(7) * (35 cm)^2 * 50 cm \\\\\tt:\implies x = (22* 35 cm * 35 cm )/(7) * 50 cm \\\\\underline{\boxed{\red{\tt \longmapsto Volume_(fill ) = 192,500 cm^3}}}`

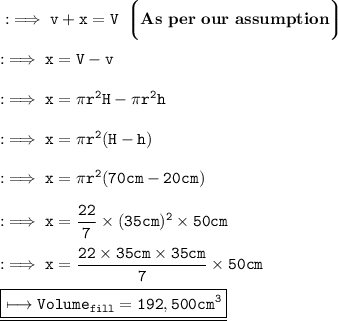
Hence the required volume of water to be filled is 192,500 cm³.