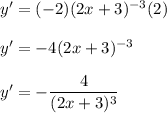Question

This one as well. Thanks! #22 a & b ​

Answer 1

22a. Answer: y' = 90x + 33

Explanation:

y = 5u² + u - 1 u = 3x + 1

First take the derivative of y = 5u² + u - 1 with respect to u
`\bigg((dy)/(du)\bigg)`

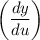
y' = (2)(5u)(u') + (1)(u') - 0

= (10u)u' + u'

Next, take the derivative of u = 3x + 1 with respect to x
`\bigg((du)/(dx)\bigg)`

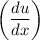
u' = 3 + 0

u' = 3

Now, input u = 3x + 1 and u' = 3 into the y' equation:

y' = (10u)u' + u'

= 10(3x + 1)(3) + 3

= 30(3x + 1) + 3

= 90x + 30 + 3

= 90x + 33

***********************************************************************

22b. Answer:
`\bold{y'=-(4)/((2x+3)^(3))}`

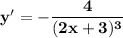
Explanation:

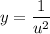`y=(1)/(u^2)` u = 2x + 3

`\text{We can rewrite y as }y=u^(-2)\\\text{Take the derivative of }y=u^(-2)\text{ with respect to u}\ \bigg((dy)/(du)\bigg)\\\\y'=(-2)(u^(-3))(u')`

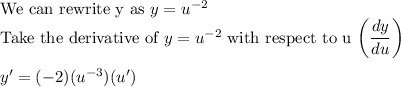
Next, take the derivative of u = 2x + 3 with respect to x
`\bigg((du)/(dx)\bigg)`

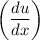
u' = 2 + 0

u' = 2

Now, input u = 2x + 3 and u' = 2 into the y' equation

`y'=(-2)(2x+3)^(-3)(2)\\\\y'=-4(2x+3)^(-3)\\\\y'=-(4)/((2x+3)^(3))`

Answer 2

• y' = 90x +33
• y' = -4/(2x +3)^3

Explanation:

The chain rule says ...

dy/dx = (dy/du)·(du/dx)

For these problems that means ...

a. dy/dx = (10u +1)·(3) = 10((3x +1) +1)(3) = 3(30x +11)

dy/dx = 90x + 33

___

b. dy/dx = -2u^-3·(2)

dy/dx = -4/(2x +3)^3