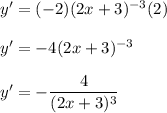22a. Answer: y' = 90x + 33
Explanation:
y = 5u² + u - 1 u = 3x + 1
First take the derivative of y = 5u² + u - 1 with respect to u
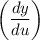
y' = (2)(5u)(u') + (1)(u') - 0
= (10u)u' + u'
Next, take the derivative of u = 3x + 1 with respect to x
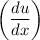
u' = 3 + 0
u' = 3
Now, input u = 3x + 1 and u' = 3 into the y' equation:
y' = (10u)u' + u'
= 10(3x + 1)(3) + 3
= 30(3x + 1) + 3
= 90x + 30 + 3
= 90x + 33
***********************************************************************
22b. Answer:
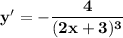
Explanation:
 u = 2x + 3
u = 2x + 3
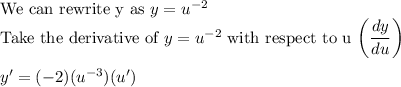
Next, take the derivative of u = 2x + 3 with respect to x
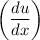
u' = 2 + 0
u' = 2
Now, input u = 2x + 3 and u' = 2 into the y' equation