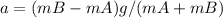Question

The system shown to the right is a standard Atwood machine. if the mass of B is 6.25 kg and the mass of A is 1.38 kg, how fast is block B accelerating?​

Answer 1

The acceleration 'a' of Block B is 6.26
`ms^(-2)`.

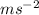Step-by-Step Explanation:

The mass of Block B is more than Block A so under the influence of gravitational acceleration 'g' = 9.8
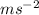`ms^(-2)` The system will move such that Block B moves downward and Block A moves upward with an acceleration 'a'.

The net force 'F' that produces this acceleration 'a' is the difference in the weights of the two blocks.

F = ma

F = (mB) g - (mA) g where mA = mass of block A , mB = mass of block B

⇒ ma = (mB) g - (mA) g where m is the total mass of the system

(mA + mB)a = (mB) g - (mA) g

Hence; acceleration 'a' is given as:

`a = (mB - mA)g/(mA + mB)`

`a = (6.25 - 1.38)9.8/(6.25+1.38)`

`a = 4.87(9.8)/7.63\\a = 47.73/7.63\\a = 6.26 ms^(-2)`

Answer 2

`6.3 m/s^2`

Step-by-step explanation:

Let's write the equations of motion for the two blocks:

`m_B g - T = m_B a\\T - m_A g = m_A a`

where

T is the tension in cable

mA = 1.38 kg is the mass of block A

mB = 6.25 kg is the mass of block B

g = 9.8 m/s^2 is the gravitational acceleration

a = ? is the acceleration of the system

Solving the first equation for T we find

`T= m_B g - m_B a`

And substituting into the second one:

`m_B g - m_B a - m_A g = m_A a\\a=(m_B - m_A)/(m_A + m_B)g=(6.25 kg - 1.38 kg)/(6.25 kg + 1.38 kg)(9.8 m/s^2)=6.3 m/s^2`