Answer:
The correct option is;
a. 20 m/s
Explanation:
The given parameters are;
The angle at which the ball is thrown, θ = 30° to the horizontal
The horizontal distance of the top edge of the building where the ball lands from where the ball is thrown, x = 20 m
The height of the top edge of the building above the throwing point = 5 meters
Let "v" represent the speed with which the ball is thrown
We have;
The vertical component of the speed with which the ball is thrown,
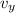 = v × sin(θ) = v × sin(30°) = v × 0.5 = 0.5·v
= v × sin(θ) = v × sin(30°) = v × 0.5 = 0.5·v
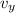 = 0.5·v
= 0.5·v
The horizontal component of the speed with which the ball is thrown, vₓ = v × cos(θ) = v × cos(30°) = v × 0.9 = 0.9·v
vₓ = 0.9·v
The kinematic equation of the motion is y =
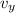 ·t - (1/2)·g·t², where;
·t - (1/2)·g·t², where;
y = The vertical height reached = 5 metes
t = The time taken to reach the specified 5 m, height
g = The acceleration due to gravity = 9.8 m/s², we have;
Therefore, we have;
5 = 0.5·v·t - (1/2)·9.8·t²...(1)
Also, from the horizontal motion of the ball, we have the following kinematic equation of motion;
x = vₓ × t
Therefore, by substituting the known values, we have;
20 = 0.9·v × t
∴ v = 20/(0.9·t) = 200/(9·t)...(2)
Substituting the value of t in equation (1) gives;
5 = 0.5·v·t - (1/2)·9.8·t² = 0.5·(200/(9·t))·t - (1/2)·9.8·t²
∴ 5 = 0.5·(200/(9·t))·t - (1/2)·9.8·t² = 100/9 - 4.9·t²
4.9·t² = 100/9 - 5 = 55/9
t = √(55/(9 × 4.9)) ≈ 1.116766
The time taken to reach the specified 5 m height = t ≈ 1.116766 seconds
From equation (2), we have, v = 200/(9·t) = 200/(9 × 1.116766) ≈ 19.8987 m/s
The speed with which the ball is thrown = v ≈ 19.8987 m/s ≈ 20 m/s. to the nearest whole number.
The speed with which the ball is thrown is approximately 20 m/s