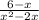Answer:
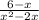
Explanation:
Find the least common multiple (LCM) of the denominators. This is:
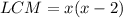
Divide the LCM by each denominator and multiply the result by each numerator, then you obtain:

Apply the distributive property, then you obtain:
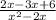
Add like terms, then you obtain: