Answer:
The formula is dimensionally consistent
Step-by-step explanation:
Dimensional Analysis
There are three fundamental magnitudes in Physics:
L = Length
T = Time
M = Mass
All the formulas and equations that use physical magnitudes must be consistent in their units.
For example, the formula:
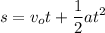
Is used to calculate the distance traveled by an object, knowing its initial speed vo, acceleration a, and time t.
The units for each magnitude are:
s = L
vo = L/T or

a = L/T^2 or
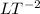
Let's analyze the dimensions of the magnitudes in the formula (the constant 1/2 is neglected because it doesn't affect the dimensional analysis):

The first term simplifies to L because the T's simplify. The same happens with the second term, the squared T's simplify:
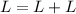
Thus the formula is dimensionally consistent