Answer:
0.9067
Explanation:
The formula used for correlation coefficient is given by,
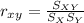
where
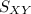 = Sample Covariance between X and Y
= Sample Covariance between X and Y
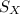 = Standard Deviation of X
= Standard Deviation of X
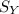 = Standard deviation of Y
= Standard deviation of Y
Sample Covariance can be calculate using formula:
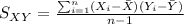
where,
 = Mean of X
= Mean of X
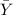 = Mean of Y
= Mean of Y
Standard Deviation is the square root of sum of square of the distance of observation from the mean.

where,
 is mean of the distribution.
is mean of the distribution.
Calculating all values:
 = -1.111
= -1.111
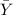 = 4.939
= 4.939
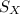 = 954.889
= 954.889
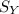 = 16.534
= 16.534
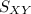 = 119.639
= 119.639
Now, Putting all values in Formula of Co rrelation Coefficient. We get,
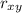 = 0.9067
= 0.9067