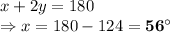Answer:
16.
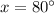
17.
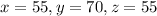
18.
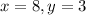
19.
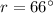 ,
,
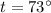
20.
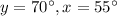
21.
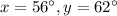
Explanation:
16. Side
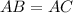
So, the opposite angles of the triangle will also be equal.
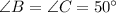
Using triangle sum property, angle of all the internal angles of a triangle is equal to
 .
.
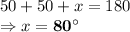
17. Two sides are given as equal,

Angles on a straight line are always equal to
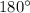 .
.
So,
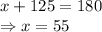
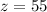
Using triangle sum property, angle of all the internal angles of a triangle is equal to
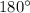 .
.

18. All the angles are given equal to each other, therefore all the sides of the triangle will also be equal to each other.

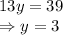
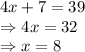
19. Two sides are given equal to each other, therefore angles opposite to them will be equal.
Using the triangle sum property in the left triangle:
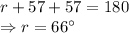
Using the property that vertically opposite angles are equal and the triangle sum property in the right triangle.
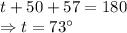
20. All the sides are given equal to each other.
So, all the angles will be equal to
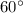 .
.


21. Angles on a straight line are always equal to
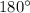 .
.
Angles opposite to equal sides in a triangle are also equal.
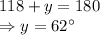
Using triangle sum property: