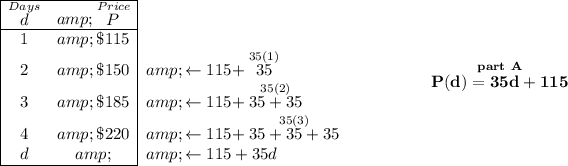
part B)
the slope is always in a linear equation, the coefficient of the independent variable, in this case namely "35".
35 or 35/1 dollars/day means
for every passing day the car is rented out, the charge is $35, so if you rent the car "d" days, you'll be charged 35d.