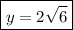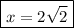Question

Analyze the diagram below and complete the instructions that follow.

Find the value of x and the value of y.
A. x=22/2, y = 8
B. X= 2, y = 416
C. x=21/2, y= 2/6
D. x= 23, y = 613

Answer 1

`\displaystyle y=2√(6)`

`\displaystyle x=2√(2)`

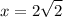
Explanation:

Trigonometric Ratios

The ratios of the sides of a right triangle are called trigonometric ratios.

The longest side of the right triangle is called the hypotenuse and the other two sides are the legs.

Selecting any of the acute angles as a reference, it has an adjacent side and an opposite side. The trigonometric ratios are defined upon those sides.

The image provided shows a right triangle whose hypotenuse is given. We are required to find the value of both legs.

Let's pick the angle of 30°. Its adjacent side is y. We can use the cosine ration, which is defined as follows:

`\displaystyle \cos 30^\circ=\frac{\text{adjacent leg}}{\text{hypotenuse}}`

`\displaystyle \cos 30^\circ=(y)/(4√(2))`

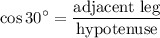
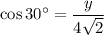
Solving for y:

`y=4√(2)\cos 30^\circ`

Since:

`\cos 30^\circ=(√(3))/(2)`

`\displaystyle y=4√(2)(√(3))/(2)`

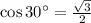
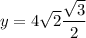
Simplifying:

`\displaystyle y=2√(6)`

Now we use the sine ratio:

`\displaystyle \sin 30^\circ=\frac{\text{opposite leg}}{\text{hypotenuse}}`

`\displaystyle \sin 30^\circ=(x)/(4√(2))`

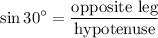
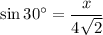
Solving for x:

`x=4√(2)\sin 30^\circ`

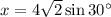
Since:

`\sin 30^\circ=(1)/(2):`

`\displaystyle x=4√(2)(1)/(2)`

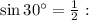
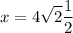
Simplifying:

`\displaystyle x=2√(2)`

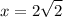
The choices are not clear, but it seems like the correct answer is C.

`\boxed{\displaystyle y=2√(6)}`

`\boxed{\displaystyle x=2√(2)}`