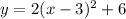Question

Given the vertex of (3, 6) of a quadratic and a point at (4,8) what would be the a value for the quadratic?


`y = a(x-h)^(2) + k`

a = ?

Answer 1

`a = 2`

`y = 2(x-3) ^ 2 +6`

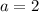
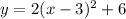
Explanation:

We have the following quadratic equation in vertex form:

`y = a(x-h) ^ 2 + k`

Where
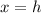`x = h` is the vertex of the parabola.

They give us the vertice:

(3, 6)

So:

`h = 3\\k = 6`

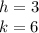
Therefore the equation is of the form:

`y = a(x-3) ^ 2 +6`

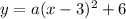
Now we need to find the value of a.

We have another point that belongs to the equation: (4, 8)

Then we substitute the values in the equation and clear a.

`8 = a(4-3) ^ 2 +6\\\\8 - 6 = a\\\\a = 2`.

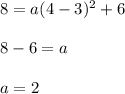Finally the equation is:

`y = 2(x-3) ^ 2 +6`

Answer 2

a = 2

Explanation:

The vertex form y = a(x - h)^2 + k

Where (h, k) is the vertex.

Given: (h, k) = (3, 6) and point (4, 8)

Now plug in the given values and find the value of "a"

x =4 and y = 8

8 = a(4 - 3)^2 + 6

8 = a(1)^2 + 6

8 = a + 6

a = 8 - 6

a = 2

So the value of a = 2.

Hope you will understand the concept.

Thank you.