Question

Find the derivative of a✓tan(5x-7)​

Answer 1

`\displaystyle y' = (5a \sec^2 (5x - 7))/(√(\tan (5x - 7)))`

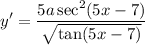
General Formulas and Concepts:

Calculus

Differentiation

• Derivatives
• Derivative Notation

Derivative Property [Multiplied Constant]:
`\displaystyle (d)/(dx) [cf(x)] = c \cdot f'(x)`

Derivative Property [Addition/Subtraction]:
`\displaystyle (d)/(dx)[f(x) + g(x)] = (d)/(dx)[f(x)] + (d)/(dx)[g(x)]`

Basic Power Rule:

1. f(x) = cxⁿ
2. f’(x) = c·nxⁿ⁻¹

Derivative Rule [Chain Rule]:
`\displaystyle (d)/(dx)[f(g(x))] =f'(g(x)) \cdot g'(x)`

Explanation:

*Note:

Treat a as an arbitrary constant.

Step 1: Define

Identify

`\displaystyle y = a√(\tan (5x - 7))`

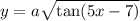
Step 2: Differentiate

1. Derivative Property [Multiplied Constant]:
   `\displaystyle y' = a(d)/(dx) \Big( √(\tan (5x - 7)) \Big)`
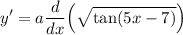
2. Basic Power Rule [Derivative Rule - Chain Rule]:
   `\displaystyle y' = (a)/(√(\tan (5x - 7))) \cdot (d)/(dx)[\tan (5x - 7)]`
3. Trigonometric Differentiation [Derivative Rule - Chain Rule]:
   `\displaystyle y' = (a \sec^2 (5x - 7))/(√(\tan (5x - 7))) \cdot (d)/(dx)[5x - 7]`
4. Basic Power Rule [Derivative Properties]:
   `\displaystyle y' = (5a \sec^2 (5x - 7))/(√(\tan (5x - 7)))`

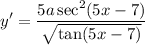
Topic: AP Calculus AB/BC (Calculus I/I + II)

Unit: Differentiation