Question

Here's a graph of a linear function. Write the equation that describes that function

Answer 1

y = 0.5x-3

Explanation:

We have given a graph of linear function.

We have to find the equation that describes that function.

y = mx+c is equation of line where m is slope and c is y-intercept.

Slope = m = y₂-y₁/x₂-x₁

From graph , we observed that

(0,-3) and (6,0) are points on graph.

Putting above values in slope formula, we have

Slope = m = 0-(-3)/6-0

Slope = m = 3 / 6

slope = m = 1/2 = 0.5

y-intercept is (0,-3).

Hence,

y = (.5)x+(-3)

y = 0.5x-3 is equation of graph that describes the linear function.

Answer 2

`y=0.5x-3`

Explanation:

We have been given graph of a linear function and we are asked to write the equation for our given graph.

We will write equation of our given function in slope-intercept form of line
`y=mx+b`, where, m represents slope of the line and b represents y-intercept or initial value of the function.

We can see from our graph that at x equals 0 y is -3, so our y-intercept or initial value of our function will be -3.

Now let us find slope of our function using slope formula.

`m=(y_2-y_1)/(x_2-x_1)`, where,

`y_2-y_1`= Difference between two y-coordinates.

`x_2-x_1`= Difference between same x-coordinates of two y-coordinates.

Upon substituting coordinates of points (0,-3) and (6,0) in slope formula we will get,

`m=(0--3)/(6-0)`

`m=(0+3)/(6)`

`m=(3)/(6)`

`m=(1)/(2)`

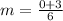
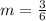
Let us substitute
`m=(1)/(2)` and b=-3 in slope-intercept form of equation.

`y=(1)/(2)x-3`

`y=0.5x-3`

Therefore, the equation
`y=0.5x-3` represents our given function.