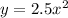Question

Graph the data in the table below. Which kind of function best models the data? write an equation to model the data.

X Y
-2 10
-1 2.5
0 0
1 2.5
2 10

Answer 1

A quadratic function.

`y=2.5x^(2)`

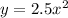
Explanation:

If you plot the points given in the table, you obtain the graph shown in the figure attached.

As you can see, it is a parabola, therefore, the function that best models the data is a quadratic function.

By definition, the parent function of a quadratic function is:

`y=x^(2)`

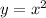
You can compress or stretch it in the y-direction by multiplying the function by a constant
`C`:

`y=Cx^(2)`

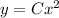
If
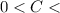`0<C<`, then the function is compressed.

If
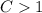`C>1`, then the function is stretched.

You can find the constant of the function asked as following:

- Substitute x=1 into the parent function to obtain the y-coordinate:

`y=(1)^(2)=1`

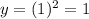
Then the point is (1,1)

- As you can see, with x=1 you obtain y=1 in the parent function, and in the function given in the table when x=1, y=2.5, therefore, the function is multiplied by 2.5. Therefore the constant is:

`C=2.5`

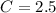
Then the function is:

`y=2.5x^(2)`