Question

Suppose that the grades of Business Mathematics and Statistic module is modeled well

by a normal probability distribution with mean (212) and standard deviation (122). Let
X be the random variable representing this distribution. Find two symmetric values "a"
and "b" such that Probability [ a

Answer 1

a = -2.57 and b = 2.57

Step-by-step explanation:

Step-by-step explanation:

Given mean of the Population = 212

Standard deviation of the Population = 122

Let X be the random variable of the Normal distribution

`Z = (x-mean)/(S.D)`

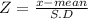
Given P( a ≤ z ≤b) = 0.99

put a=-b

P( -b ≤ z ≤b) = 0.99

⇒ |A( b) - A( -b)| =0.99

⇒ | A( b) + A( b)| =0.99

⇒ 2 |A (b)| = 0.99

⇒ | A(b)| = 0.495

From normal table find value in areas

b = 2.57 ( see in normal table)

Given a =-b

a = - 2.57