Answer:
1 -
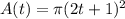 meter²
meter²
2 - 5,281 meter²
Explanation:
We are given that,
Radius of the circle is modeled by the function,
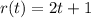 , where 't' is the time in minutes.
, where 't' is the time in minutes.
Part 1: It is required to compute the area of the forest burned.
Since, Area of the circle =
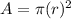
So,
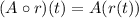
i.e.
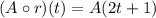
i.e.
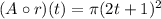
Thus, the area of the forest burned by the fire is
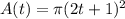 meter²
meter²
Part 2: It is required to find the area after 20 minutes of burn.
That is, t = 20 mins.
So substituting, we get,

i.e.
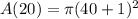
i.e.
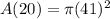
i.e.
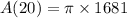
i.e.
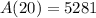 meter²
meter²
Thus, the area burned after 20 mins of fire is 5,281 meter².