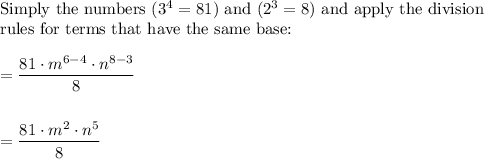Question

Quick I need the answer!

Answer 1

I think I answered this earlier too. 2nd answer

Answer 2

Answer:
`\bold{b)\ (81\cdot m^(2)\cdot n^(5))/(8)}`

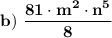
Explanation:

Use the power rule for exponents (multiply the exponents).

Then move the terms that have negative exponents to the other side of the fraction bar and change the sign of the exponent.

Then simplify and use the division rule for exponents (subtract the exponents).

`(\bigg(3\cdot m^(-1)\cdot n^2 \bigg)^4)/(\bigg( 2\cdot m^(-2)\cdot n\bigg)^3)\\\\\\\text{distribute the exponent of 4 on the top and 3 on the bottom:}\\\\=(3^4\cdot m^(-4)\cdot n^8)/(2^3\cdot m^(-6)\cdot n^3)\\\\\\\text{Move }m^(-4)\ \text{and }m^(-6)\ \text{to the other side of the fraction bar and change}\\\text{the sign of the exponent.}\\\\=(3^4\cdot m^(6)\cdot n^8)/(2^3\cdot m^(4)\cdot n^3)`

`\text{Simply the numbers }(3^4=81)\ \text{and }(2^3=8)\ \text{and apply the division}\\\text{rules for terms that have the same base:}\\\\=(81\cdot m^(6-4)\cdot n^(8-3))/(8)\\\\\\=(81\cdot m^(2)\cdot n^(5))/(8)`